Определение понятия акустический импеданс
Под акустическим импедансом понимается совокупная сопротивляемость внешней среды звуковому воздействию, которое по сути является величиной совокупности амплитуд звукового давления по отношению к скорости звука.
Имя естествоиспытателя, осуществившего ввод понятия в научный оборот, не сохранилось, но сегодня трудно представить условия современной жизни без учета данной величины.
В самом общем виде, понятие акустического импеданса, иначе комплексного акустического сопротивления окружающей среды, описывает специфическую сопротивляемость, с которой сталкивается какая-либо поверхность способная к колебаниям, например, стенкам рупора, имеющих конусовидную форму.
Вывод: от чего зависит громкость наушников и чем важен импеданс
Вот и подошло к концу очередное наше путешествие в мир электроники и основных её терминов. Надеемся, теперь вы на 100% знаете, что это такое – сопротивление (импеданс) в наушниках и как Омы влияют на технические возможности различных устройств. Давайте закрепим усвоенный материал: на громкость в первую очередь влияет чувствительность, но чтобы добиться лучшего результата, она должна согласовываться с мощностью, которая в свою очередь напрямую зависит от импеданса. Так что внимательно смотрите на цифру после значка «Ω» в спецификации или на упаковке перед покупкой – это упростит принятие окончательного
Share Tweet Email Pin
Формула акустического импеданса
Формула акустического импеданса достаточно проста, и должно быть известна всем музыкантам и даже многим школьникам из школьного курса физики – Za = Ra+iXa.
Разберем подробно вышеуказанную формулу.
Под буквой i понимается так называемая «мнимая единица», под которой в своею очередь понимается особое число, относящееся к виду комплексных чисел, квадрат которого неизменно составляет значение -1.
Под Ra понимается само звуковое сопротивление, определяется процессами переходов энергии из упорядоченных процессов в неупорядоченные процессы, чаще определяемые в физике как диссипация, и неизбежными потерями значительной части звуковых волн на их излучение.
Под Xa понимается так называемая мнимая составляющая, то что чаще именуют реактивной формой звукового сопротивления, которое в значительной мере определяется теми же явлениями перехода энергии из неупорядоченных в упорядоченные процессы в звуковой системе, что является прямым следствием обладания этой системой различных инерционных сил и сил упругости.
Исходя из всего вышесказанного, специалистами проводится деление видов реактивного сопротивления на инерционное и упругое.
Если взглянуть на международную систему измерений, так называемую систему СИ, единицей данной величины является величина равная одному Ньютону умноженному на секунду разделенное на сантиметр в пятой степени.
До принятия международной системы измерения широко использовалась так называемая система «сантиметр-грамм-секунда», также известная как просто «СГС».
В данной системе формула высчитывания единицы акустического импеданса практически идентична способу высчитывания в системе СИ, только вместо Ньютона использовалась «Дина», совершенно особая единица, равная величине силы, сообщаемой телу, имеющему массу в один грамм скорость в один сантиметр в секунду. Самым старым значением и синонимом понятия акустический импеданс является «акустический ом».
Сопротивление колонок, какой параметр выбрать
Акустические системы состоят в основном из усилителей мощности, частотных разделительных фильтров и громкоговорителей.
Пропускная способность составляет 20-20 000 Гц. Усилители мощности бывают широкополосные и разделённые по диапазону частот.
- Низкочастотные (20–300 Гц).
- Среднечастотные (300–5000 Гц).
- Высокочастотные (5 000–20 000 Гц) относятся к классу 3 полосных.
Усилители 2 полосные имеют два диапазона частот НЧ-СЧ и ВЧ. Входной сигнал распределяется фильтрами по частотным каналам и поступает на соответствующие усилители.
Радиолюбителям для расчёта разделительных фильтров необходимо знать входной импеданс на разных частотных диапазонах. Для низких частот активное сопротивление громкоговорителя равно 4 или 8 Ом. Импеданс можно принять равным примерно на 10% от этих величин.
Можно его измерить, подключив генератор звуковой частоты, настроенный на частоту раздела (не ниже 6 к Гц) через резистор 1 ком к громкоговорителю. Отношение напряжений на резисторе и громкоговорителе покажет искомую величину. Таким же способом находится импеданс высокочастотной головки.

Где применяется
Данное понятие применяется в различных разделах физики, механики, математики и некоторых междисциплинарных исследованиях, в которых в том или ином виде присутствуют эти дисциплины.
Не менее часто это понятие используется на производствах и при различных видах проектирования. Величина акустического импеданса учитывается при проектировке и сборке различных излучателей, звуковых приемников, мембранных поверхностей, распределителей и т.д.
Для специалистов занимающихся свойствами излучающих систем данное понятие необходимо для расчетов мощностей излучения и различных условий, сопротивляемости волновому воздействию объектов внешней среды.
Особенности подключения звуковых колонок
Подключение нескольких акустических систем к источнику сигнала осуществляется последовательным, параллельным и параллельно-последовательным способом. Соответственно, параметр группы динамиков вычисляется по Закону Ома. На этикетках и в инструкциях по эксплуатации динамиков, наушников указывается их сопротивление (4,8,16 Ом). Если ваши колонки не новые, утеряна инструкция по эксплуатации или по другой причине сопротивление колонок вам неизвестно, его можно измерить мультиметром. Что это такое? Это специальный прибор для измерения данного параметра.
Освободив динамики в колонках от аппаратуры, замеряете их сопротивление. Мультиметр будет показывать несколько заниженные значения сопротивлений близкие стандартным.
Подпишитесь на наши Социальные сети
Ограничения
Понятие импеданса применимо, если при приложении к двухполюснику гармонического напряжения, ток, вызванный этим напряжением, также гармонический той же частоты. Для этого необходимо и достаточно, чтобы двухполюсник был линейным и его свойства не менялись со временем. Если это условие не выполнено, то импеданс не может быть найден по следующей причине: невозможно получить выражение для импеданса, не зависящее
от времени
t
, поскольку при вычислении импеданса множитель e j ω t {\displaystyle e^{j\omega t}} в (1) не сокращается.
- Однако и для линейных двухполюсников (для которых зависимость от времени сокращается) импеданс всё же зависит от частоты (за исключением случая когда двухполюсник сводится к схеме из одних резисторов и импеданс оказывается действительной величиной).
Практически это означает, что импеданс может быть вычислен для любого двухполюсника, состоящего из резисторов, катушек индуктивности и конденсаторов, то есть из линейных пассивных элементов. Также импеданс хорошо применим для активных цепей, линейных в широком диапазоне входных сигналов (например, цепи на основе операционных усилителей). Для цепей, импеданс которых не может быть найден в силу указанного выше ограничения, бывает полезным найти импеданс в малосигнальном приближении для конкретной рабочей точки. Для этого необходимо перейти к эквивалентной схеме и искать импеданс для неё.
Обобщенный импеданс в s-плоскости и преобразование Лапласа[ | ]
Импедансы, определённые через комплексную частоту j ω {\displaystyle j\omega } , позволяют вычислять частотный отклик некоторой линейной цепи, возбуждаемой гармоническим сигналом, причём только в установившемся режиме. Для расчёта отклика цепи на сигнал, произвольно изменяющийся во времени применяется обобщенный импеданс — функции комплексной переменной s = σ + j ω {\displaystyle s=\sigma +j\omega } и отклик цепи во временно́й области вычисляется через обратное преобразование Лапласа, причем в таких вычислениях возбуждающий сигнал f i n ( t ) {\displaystyle f_{in}(t)} из временного представления должен быть предварительно преобразован в комплексное представление F t ( s ) {\displaystyle F_{t}(s)} через прямое преобразование Лапласа:
F t ( s ) = ∫ 0 ∞ f i n ( t ) e − s t d t . {\displaystyle F_{t}(s)=\int _{0}^{\infty }f_{in}(t)e^{-st}\,dt.}
Комплексный отклик системы выражается обычным способом через преобразованное комплексное представление возбуждающего сигнала и комплексную передаточную функцию системы H ( s ) {\displaystyle H(s)} :
F t , H ( s ) = H ( s ) F t ( s ) . {\displaystyle F_{t,H}(s)=H(s)\ F_{t}(s).}
| Двухполюсник | Обобщённый импеданс |
| Резистор | R {\displaystyle R\,} |
| Катушка индуктивности | s L {\displaystyle sL\,} |
| Конденсатор | 1 s C {\displaystyle {\frac {1}{sC}}\,} |
Комплексная передаточная функция вычисляется обычным методом расчёта электрических цепей, например, по правилам Кирхгофа, в формулы в качестве сопротивлений подставляются обобщённые импедансы. Обобщённые импедансы пассивных двухполюсников приведены в таблице. Например, обобщённый импеданс цепи, состоящей из последовательно включённых резистора и катушки индуктивности будет R + s L {\displaystyle R+sL} .
Отклик цепи во временно́й области вычисляется обратным преобразованием Лапласа:
f F , H ( t ) = L − 1 [ H ( s ) F t ( s ) ] = 1 2 π i ∫ σ 1 − j ⋅ ∞ σ 1 + j ⋅ ∞ e s t H ( s ) F t ( s ) d s , {\displaystyle f_{F,H}(t)={\mathcal {L}}^{-1}[H(s)\ F_{t}(s)]={\frac {1}{2\pi i}}\int \limits _{\sigma _{1}-j\cdot \infty }^{\sigma _{1}+j\cdot \infty }e^{st}H(s)\ F_{t}(s)\,ds,} где σ 1 {\displaystyle \sigma _{1}\ } — некоторое вещественное число, выбираемое из условий сходимости интеграла. Пример вычисления временно́го отклика RC-фильтра нижних частот на ступенчатое возмущение Пассивный RС-фильтр нижних частот 1-го порядка
Простейший фильтр нижних частот 1-го порядка изображён на рисунке и состоит из последовательно соединённых резистора и конденсатора, образующего делитель напряжения для входного сигнала где выходной сигнал снимается с конденсатора, обобщённый комплексный коэффициент передачи H R C ( s ) {\displaystyle H_{RC}(s)} такого делителя:
H R C ( s ) = 1 / s C R + 1 / s C = 1 s R C + 1 = 1 s T + 1 , {\displaystyle H_{RC}(s)={\frac {1/sC}{R+1/sC}}={\frac {1}{sRC+1}}={\frac {1}{sT+1}},} где обозначено T = R C {\displaystyle T=RC} — постоянная времени RС-цепи.
Ступенчатый входной сигнал можно выразить через функцию Хевисайда h ( t ) {\displaystyle h(t)} :
U i n ( t ) = U 0 h ( t ) , {\displaystyle U_{in}(t)=U_{0}\ h(t),} где U 0 {\displaystyle U_{0}} — амплитуда ступеньки.
Преобразование Лапласа входного сигнала:
F i n ( s ) = L [ U 0 h ( t ) ] = ∫ 0 ∞ e − s t U 0 h ( t ) d t = U 0 / s . {\displaystyle F_{in}(s)={\mathcal {L}}[U_{0}\ h(t)]=\int \limits _{0}^{\infty }e^{-st}\,U_{0}\,h(t)\,dt=U_{0}/s.}
U o u t ( t ) = L − 1 [ H R C ( s ) F i n ( s ) ] = 1 2 π i ∫ σ 1 − j ⋅ ∞ σ 1 + j ⋅ ∞ e s t 1 s T + 1 ⋅ U 0 s d s = U 0 ( 1 − e − t / T ) . {\displaystyle U_{out}(t)={\mathcal {L}}^{-1}[H_{RC}(s)\ F_{in}(s)]={\frac {1}{2\pi i}}\int \limits _{\sigma _{1}-j\cdot \infty }^{\sigma _{1}+j\cdot \infty }e^{st}{\frac {1}{sT+1}}\cdot {\frac {U_{0}}{s}}\,ds=U_{0}(1-e^{-t/T}).}
Таким образом, получен отклик цепи при нулевом начальном условии ( U C = 0 {\displaystyle U_{C}=0} при t = 0 {\displaystyle t=0} ), такой же, как и при применении другого метода расчёта, например, из решения обыкновенного дифференциального уравнения.
Для практического применения расчета цепей (и других расчётов) составлены подробные таблицы прямого и обратного преобразования Лапласа многих часто встречающихся при расчётах функций.
Комбинируя преобразование Лапласа с использованием его свойств и интеграл Дюамеля обычно относительно легко найти отклики во временной области самых различных линейных электрических цепей.
Физический смысл
Алгебраическая форма
Если рассматривать комплексный импеданс как комплексное число в алгебраической форме, то действительная
часть соответствует активному сопротивлению, а
мнимая
— реактивному. То есть двухполюсник с импедансом z ^ ( j ω ) {\displaystyle {\hat {z}}(j\omega )\;} можно рассматривать как последовательно соединенные резистор с сопротивлением ℜ ( z ^ ( j ω ) ) {\displaystyle \Re ({\hat {z}}(j\omega ))} и чисто реактивный элемент с импедансом ℑ ( z ^ ( j ω ) ) {\displaystyle \Im ({\hat {z}}(j\omega ))}
Рассмотрение действительной части полезно при расчёте мощности, выделяемой в двухполюснике, поскольку мощность выделяется только на активном сопротивлении.
Тригонометрическая форма

Пример графического представление импеданса на комплексной плоскости
Если рассматривать импеданс как комплексное число в тригонометрической форме, то модуль
соответствует отношению амплитуд напряжения и тока (сдвиг фаз не учитывается), а
аргумент
— сдвигу фазы между током и напряжением, то есть на сколько фаза тока
отстаёт
от фазы напряжения или
опережает
.
Семь раз отмерь
Это означает, что при том же положении регулятора громкости выходной ток будет в 1. Это на первый взгляд вроде бы и ничего, если регулятор больше, чем наполовину не выкручивать, однако есть нюансик. Так как сопротивление меньше, то при той же выходной мощности на колонке, мощность рассеиваемая на выходном каскаде усилителя будет заметно больше, в 1. Резистор на 50 Ватт, ага! Тогда уж лампочку от автомобильной фары, заодно цветомузыка будет. Только придется эту всю хрень зашунтировать RC-цепочкой, чтобы средние-высокие частоты худо-бедно воспроизводились. Можно усилок спалить, если перегреется и нет защиты.
Пассивные колонки (а это большинство колонок) требуют отдельных Импеданс — это уровень сопротивления потоку электрического сигнала и.
Что такое импеданс и как электрическая фаза влияет на звук наушников
Читая мои обзоры, несложно заметить, что я уже много лет с интересом слежу за продукцией киевской лаборатории Ambient Acoustics — кастомными внутриканальными мониторами (так называют наушники, сделанные из акрила по слепку ушей конкретных пользователей, подробнее можете прочитать тут). Наращивая сложность и качество своих изделий, сотрудники лаборатории не забывают и про исследовательскую работу. Недавно они представили совершенно новую технологию коррекции фазы и импеданса в своих наушниках, предлагаю разобраться, что это и зачем оно надо.

Я расспросил представителей лаборатории о том, как работает их технология, и на основе их рассказов постарался написать объяснение.
Для начала нам необходимо четко понять, как работают наушники. Я когда-то писал достаточно большую статью на эту тему, поэтому изложу кратко. В основе практически всех излучателей, использующихся в наушниках, лежит принцип преобразования электрической энергии в механическую с помощью постоянных и переменных магнитов. То есть через проводник, помещенный в постоянное магнитное поле, проходит электрический сигнал, что вызывает появление вокруг него переменного магнитного поля. Два этих поля взаимодействуют, и проводник приводится в механическое движение. Это движение тем или иным способом преобразовывается в колебания воздуха, которые мы и воспринимаем как звук.
Чтобы увеличить силу магнитного поля, проводник чаще всего сматывается в катушку. Там же, где имеется катушка индуктивности, в дело вступает интересная физическая величина под названием реактивное сопротивление. В отличие от обычного сопротивления резистора, характеризующегося соотношением напряжения к току, сопротивление реактивных элементов (катушек индуктивности и конденсаторов) не может быть измерено так просто. Обычное сопротивление идеальной катушки стремится к нулю, конденсатора — к бесконечности.
Для таких элементов знаменитым математиком Хевисайдом в 1886 году было введено понятие комплексного (или полного) сопротивления, называемого также импедансом. Импеданс, в отличие от сопротивления, изменяется в зависимости от частоты сигнала, проходящего через электрическую цепь. Чаще всего в характеристиках наушников указывают импеданс, для сигнала в 1 кГц.
Вывод первый: наушники обладают нелинейным импедансом, зависящим от частоты.
В то время как импеданс изменяется с частотой, то же самое происходит и с фазой. В данном случае «фаза» — это временной сдвиг между пиковыми значениями подводимого электрического напряжения и тока. Чем больше фазовый сдвиг, тем больше реактивная составляющая нагрузки. Как правило, чем больше фазовая задержка, тем труднее управлять нагрузкой. Обычный резистор имеет практически нулевую фазовую задержку во всем диапазоне звуковых частот. То есть напряжение и ток, проходящие через резистор, находятся в фазе, без временного сдвига между собой.
Динамические наушники, как правило, обладают практически линейными кривыми импеданса и фазы. Вот, например, графики для наушников Monster Turbine Pro Gold.

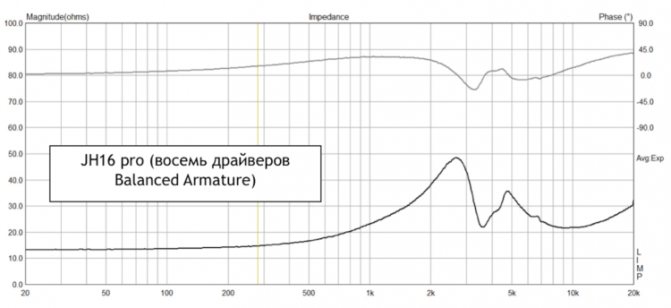
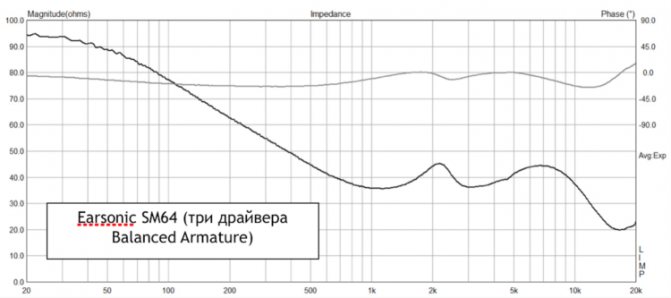
Многие внутриканальные мониторы класса high-end используют технологию уравновешенного якоря (излучатели Balanced Armature). Благодаря малым размерам излучателей есть возможность применения двух, трех и более (в некоторых случаях доходит до восьми) излучателей в одном наушнике. По аналогии со стационарными акустическими системами, в одном наушнике присутствуют: сабвуфер, «среднечастотники», «высокочастотники». Чем больше количество динамиков, тем больше количество частотных полос, на которые дробится весь слышимый частотный диапазон. Разделение осуществляется с помощью электрических фильтров (электрический кроссовер), акустических фильтров (акустический кроссовер) и акустических резонаторов (горны, обратные горны).
Арматурные излучатели сами по себе обладают достаточно «реактивной» кривой импеданса и неравномерной фазой за счет большой индуктивности катушки и постоянных магнитов во внутренней структуре. В качестве электрического кроссовера применяются пассивные электрические фильтры 1-го и 2-го порядка на основе конденсаторов, индуктивностей и резисторов. Из-за этого, кривые импеданса и фазы таких наушников могут быть какими угодно.
Вывод второй: многодрайверные арматурные наушники чаще всего обладают нелинейными графиками импеданса и фазы.
Как правило, чем равномерней кривые импеданса и электрической фазы наушников, тем меньше влияние выходного импеданса источников на итоговую частотную характеристику наушников. Таким образом, благодаря линейности электрических характеристик вставных динамических наушников, они являются наименее требовательными к источникам. И наоборот, чем больше неровности кривой импеданса наушников, тем больше выходной импеданс источника влияет на их звук. На приведенных выше графиках заметны достаточно большие всплески импедансов разных наушников, достигающие порой 80-100Ω. Как легко можно увидеть на графиках, на этих же участках АЧХ возникают задержки между изменением напряжения и тока (фаза). Именно на этих участках при наложении фазовых смещений, неравномерности импеданса наушников и выходного импеданса усилителя, обусловленного его схемотехникой, проявляются изменения в итоговых амплитудно-частотных характеристиках (АЧХ) наушников. Проще говоря, будет слышна разница между тем, как наушники должны звучать, и как они звучат на данном источнике. Отсюда возникает проблема «несыгранности» некоторых многодрайверных моделей с некоторыми усилительными трактами. Есть такое эмпирическое «правило одной восьмой»: выходной импеданс источника должен составлять не больше 1/8 импеданса наушников. То есть, для современных чувствительных наушников с импедансом в 16Ω, выходной импеданс плеера должен быть менее 2Ω, а лучше — еще меньше.
Разумеется, сейчас есть очень много хороших плееров с выходным импедансом, стремящимся к нулю и позволяющих максимально нивелировать такие проблемы, но тут есть ряд трудностей. Во-первых, близкий к нулевому импеданс позволяет снизить влияние неравномерности, но не убирает его полностью. Во-вторых, в некоторых случаях использовать такие источники не представляется возможным. Например, Ambient Acoustics очень часто делают свои мониторы для музыкантов, использующих их с профессиональным оборудованием, в котором далеко не всегда ставят за цель достижение низкого выходного импеданса.
Вернемся от теории к практике, а точнее, к Ambient Monitors. Несколько лет Ambient Acoustics постепенно двигались вперед, улучшая свои продукты, и пытаясь достичь поставленных целей. Улучшения носили как внешний (качество литья, применение разных материалов и вставок, изготовление собственных коннекторов), так и внутренний (использование печатных плат для кроссоверов, максимальное использование акустического, а не электрического демпфирования) характер.
Следующим шагом стало стремление добиться максимальной отдачи мониторов, независимо от используемого источника. Единственным способом добиться этого было обеспечить как можно большую линейность тех самых графиков импеданса и фазы.
Основной задачей было сглаживание резонансных пиков электрического контура системы драйверов и электрических кроссоверов в каждой модели, и тем самым понизить влияние внутренней схемотехники источников на итоговое звучание мониторов, повысив «натуральность» звучания. Итогом годовой работы и «обкатки» стало внедрение технологии коррекции фазы и кривой импеданса во все кастомные мониторы.
Разумеется, детали реализации технологии не раскрываются. Основной же ее особенностью является то, что она практически не влияет на итоговую АЧХ мониторов, а «работает» исключительно в области электрических параметров. Максимальной «ровности» в пределах 10 единиц (см. рисунок ниже) из всей линейки мониторов удалось достичь в студийных AM3 Reference Edition. Для остальных моделей этот показатель лежит в пределах 20-40 единиц (что также очень неплохо).

Для того чтобы проверить, как это звучит на практике, я отдал на модификацию свои Ambient Monitors AM6 HiRez. Помимо коррекции, в лаборатории мне сделали новый дизайн (белый карбон с синим корпусом и серебристыми надписями — смотрятся просто великолепно), а также сделали концы звуководов из мягкого акрила. Последнее — еще одна новая наработка компании, это позволяет добиться большего комфорта в ходе длительного ношения.

Тесты проводились с несколькими плеерами, в числе которых были: HiFiMan 901, Rio Karma, Sandisk Sansa Clip+. Также наушники прослушивались с iPhone 4, iPod Video 5.5G и ЦАП Yulong DA8.

Изменения лучше всего слышны на источниках «попроще», хотя и на топовых плеерах их можно услышать. Бас стал более упругим, ощущение удара сильнее и собранней, особенно хорошо это слышно на качественных записях ударных (те же «Ондекоза» звучат очень круто). На простых источниках ощутимо уменьшилась яркость, звук стал не таким резким, но это не в ущерб детализации. Также лучше стало построение виртуальной сцены, позиционирование источников звука — просто невероятное (на качественных записях).

Тот факт, что Ambient Monitor 6 HiRez стали лучше работать с простыми источниками звука, сложно недооценить. Я знаю некоторых людей, которым нравится звук рекордеров, и они используют их в качестве портативных плееров. Теперь с ними вполне можно использовать продукты AA. Я могу ошибиться, но, по-моему, еще никто из в мире не предлагал ничего подобного, поэтому покупка Ambient Monitors становится еще более оправданной для ценителей качественного портативного звука.